高等数学中映射概念的实例教学法

摘要 摘要: 从映射的角度阐述函数概念的发展历程，给出了密码学、通信领域以及哲学层面上的一些映射概念的实例，其目的是尽量挖掘数学基础知识与学生所学专业的联系，使数学联系生

　　摘要: 从映射的角度阐述函数概念的发展历程，给出了密码学、通信领域以及哲学层面上的一些映射概念的实例，其目的是尽量挖掘数学基础知识与学生所学专业的联系，使数学联系生活、数学联系科技、数学联系哲学，进而激发学生的求知欲，发挥其主动学习的潜能.

　　关键词: 映射; 函数; 狄利克雷函数; 移位密码; 信源编码; 一一映射

　　0 引言

　　高等数学的知识内容是其他一些数学课和专业课的基础，是学生后续学习中的“必备知识”，但这种必要性对于刚入学的学生而言却有些模糊，老师只能从宏观上加以介绍，学生很难有深刻体会，因而作为大学数学中最基础、最重要的数学课程之一，高等数学常常被冠以“枯燥难学”的标签. 而高等数学让学生望而生畏的重要原因之一，是其中的许多概念与学生的专业相去甚远. 针对这种状况，我们在教学中作了一些探索和尝试，尽量挖掘基础知识和基本概念与专业的联系，旨在让抽象的数学概念回溯到它的现实源头，从而使它与人的固有经验相衔接，进而激发学生的求知欲，发挥其主动学习的潜能.

　　数学被认为是描述自然界最好的语言，伽利略曾经说过“大自然这部巨著是用数学语言写成的”，但大自然是丰富多彩、千变万化的，怎么办? 数字化是用数学方法研究物质世界的前提，而映射是实现数字化的关键. 事实上函数作为高等数学的重要研究对象，是映射的一种特殊情况. 映射反映了事物之间的“一对一”或“多对一”的依赖关系，可以说映射无处不在. 比如我们每个人都有唯一对应的身份证号，学生进大学之后每个人对应着一个学号，坐在教室里的每个人和教室的座位之间等都存在着特殊的对应关系，抛开它们的实际意义，这种对应关系实质上就是数学中的“映射”.

　　高等数学学习的四种境界分别是: 数学联系生活以感受数学; 数学联系科技以应用数学; 数学联系艺术以欣赏数学; 数学联系哲学以透视数学. 相应地，教师在教授数学知识的时候也要设法从这四个角度加以引导. 因此在介绍映射概念的时候，结合简单的加密体制、通信中的编码理论以及哲学思想，为学生介绍了一些活生生的“映射”的实例，不仅使学生从日常生活、专业以及哲学这几个不同的层次对“映射”这一概念本身有了深刻的理解，同时也充分意识到“映射”作为现代数学的一个基本概念，对我们用数学方法研究客观世界功不可没.

　　1 映射的基本概念

　　定义 1 [1] 设 X、Y 是两个非空集合，如果存在一个对应法则 f，使得对 X 中每个元素 x，按法则 f，在 Y 中都有唯一确定的元素 y 与之对应，那么称 f 为从 X 到 Y 的映射，记作 f: X→Y. 集合 X 称为映射 f 的定义域，记为 Df，即 Df = X; X 中所有元素的像组成的集合称为映射 f 的值域，记作 Rf，则 RfY.如果对任意的 x1≠x2，都有 f( x1 ) ≠f( x2 ) ，则称 f 为单射; 如果 Rf = Y，则称 f 为满射. 如果 f 既是单射又是满射，则称 f 为一一映射.定义 2 [1] 设 f 是集合 X 到 Y 的单射，则由定义，对每个 y∈Rf，都有唯一的 x∈X，使得 f( x) = y. 于是可以定义一个从 Rf 到 X 的新映射 g: Rf→X，对每个 y∈Rf，规定 g( y) = x，其中 x 满足 f( x) = y，则称映射 g 为 f的逆映射，记作 f - 1 ，其中 Df - 1 = Rf，Rf - 1 = X.

　　2 映射的实例探究

　　2. 1 从映射角度阐述函数概念的意义

　　微积分理论是为了解决有关运动或变化的实际问题而引进的，因此在微积分诞生初期，函数也打上了实际背景的烙印，绝大部分函数是被当作曲线来研究的. 后来，欧拉给出了函数的解析表达式定义，即一个变量的函数是由这个变量和一些数，即常数，以任何方式组成的解析表达式. 1822 年，法国数学家傅里叶发现某些函数可用曲线表示，也可用一个或多个式子表示，从而结束了函数概念是否以唯一一个式子表示的争论，把对函数的认识又推进了一个新的层次. 1837 年，德国数学家狄利克雷认为怎样去建立 x 与 y 之间的关系无关紧要，他拓广了函数概念，指出: “对于在某区间上的每一个确定的 x 值，y 都有一个或多个确定的值，那么 y 叫做 x 的函数. ”在康托建立了集合论之后，美国数学家维布伦用“集合”和“对应”的概念给出了近代函数定义，通过集合概念，把函数的对应关系、定义域及值域进一步具体化了，并且打破了“变量是数”的极限，变量可以是数，也可以是其他对象( 点、线、面、体、向量、矩阵等) ，现代函数的定义就是从映射的角度来阐述的，即定义 3 [2]设数集 DR，则称映射 f: D→R 为定义在 D 上的函数，通常简记为 y = f( x) ，x∈D，其中 x 称为自变量，y 称为因变量，D 称为定义域，记为 Df，即 Df = D.在上述定义下，从映射的角度出发，不难理解狄利克雷函数的属性及意义.例 1 狄利克雷函数 D( x) = 1， x∈Q {0， x∈R Q.狄利克雷函数的提出，将数学从研究函数的“计算”转变到研究函数的“概念、性质和结构”，撇开了函数的运动变化的属性，强调了函数是变量与变量之间的对应关系.

　　2. 2 密码中的映射实例

　　密码学用于保护军事和外交通信可以追溯到几千年前，在今天的信息时代，大量敏感信息如病历、法庭记录、商业信息常常要通过公共设施或计算机网络来进行交换，所以密码在现代社会更为重要. 众所周知，密码和数学密不可分，1976 年 DIFFIE 和 HELLMAN 在《密码学新方向》一文中给出了非对称密码算法的思想[3]，开启了现代密码学的大门，现代密码学是建立在数论( 初等数论、解析数论、代数数论) 、计算复杂性分析、计算机算法、信息论等诸多数学分支上，与数学的关系更为密切，但最早的密码———移位密码，其本质就是简单的映射.例 2 设集合 A 是 26 个英文字母构成的集合，即 A = { a，b，c，…，x，y，z} ，建立集合 A 到自身的映射 f: A→A 如下: f( a) = b，f( b) = c，f( c) = d，…，f( y) = z，f( z) = a.上述映射的定义域是和值域都是 A，该映射既是单射也是满射，是一一映射. 这个映射给出了一个特殊的移位密码，比如明文“calculus”，经过映射 f 加密: f( c) = d，f( a) = b，f( l) = m，f( c) = d，f( u) = v，f( s) = t，得到的密文为“dbmdvmvt ”，而从密文恢复出明文的过程就是按照 f 的逆映射，从“像”得到“原像”的过程，换句话说，加密和解密的过程实质上是映射和逆映射的关系.

　　2. 3 通信中的映射实例

　　在通信过程中，消息一般不能直接传送而是要通过一定形式的电磁信号来传送. 由消息变成信号的运算称为编码，当信号被接收后还需还原成消息，由接收信号还原成消息的运算称为译码. 编码、译码事实上也是特殊的映射. 在通信工程中，常用的信源编码有两大类型，即定长编码和变长编码，下面是一个简单的定长编码的例子.例 3 设集合 A 是空格( 用“ ”表示) 和 26 个英文字母构成的集合，即 A = { ，a，b，c，…，x，y，z} ，集合 B 为数字 0 到 31 构成的集合，即 B = { 0，1，2，…，31} ，集合 C 为集合 B 中所对应元素的二进制表示，即 C = { 00000，00001，00011，…，11111} ，则可建立集合 A 与集合 B 之间的映射 f : A →B，即 f: |→0，同时将字母对应到其在字母表中的顺序数字，即 f( a) = 1，f( b) = 2，f( c) = 3，…，f( z) = 26; 而集合 B 和集合 C 之间可建立映射 g: B→C，将 B 中的元素对应到其二进制表示，即 g( 0) = 00000，g( 1) = 00001 ，…，g( 26) =11010，g( 27) = 11011，…，g( 31) = 11111.在上述意义下，映射 f 和映射 g 都是单射，而且它们可以构成复合映射 g  f: A→C，即 g  f( ) = 00000，g  f( a) = 00001，…，g  f( z) = 11010.在上述映射中，映射 f，g，g  f 均为单射，但映射 f，g  f 不是满射.比如我们可以把“calculus”这 8 个字母按照其在字母表的顺序先和数字“3 1 12 3 21 12 21 19”建立对应关系，进一步将其对应为 8 个二进制码“00011 00001 01100 00011 10101 01100 10101 10011”在二进制信道中传输，这是信道编码的基础.

　　2. 4 映射的哲学实例

　　我国著名数学教育家徐利治曾说过: 哲学是数学更深刻的思想基础[4]. 这是与高等数学课程的特点紧密联系的，微积分理论并不是凭空来的，它是来源于实践又反过来服务于实践的，正是基于此，克莱因强调: 作为教和学的数学，应该是发明、发现中的数学，是生长形成中的数学. 微积分既是一种理论，也是一种方法，微积分的思想在我国古代的许多名言中都有所体现，比如老子的“合抱之木，生于毫末; 九层之台，起于累土; 千里之行，始于足下”，荀子的“不积跬步无以至千里，不积小流无以成江河”. 微积分的研究对象从静止到了运动，从直线到了曲线，从常量到了变量，从有限延伸到无限，这些研究对象之间是对立统一的矛盾体，因此借助静止研究运动、借助有限研究无限，以直代曲、以不变代变的辩证的思想方法在高等数学的许多概念理论中都有重要体现，我们不妨从一个具体的例子出发来体会其重要性.

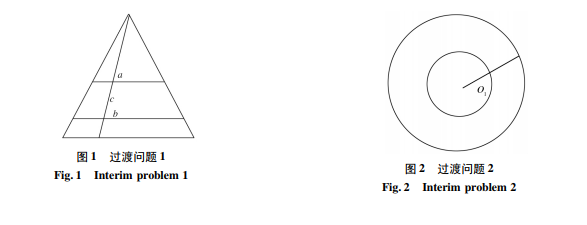
　　例 4 “方寸嵌宇宙，滴水含太阳”[5]的数学解释.分析: “方寸嵌宇宙，滴水含太阳”和英国浪漫主义诗人布莱克的“一沙一世界，一花一天堂”有异曲同工之妙，其中蕴含着丰富的哲学原理. 当我们从数学的角度、量化的观点分析这句话的时候，则蕴含着局部与整体的一种辩证关系. 我们知道，对有限集合而言，如果局部是整体的真子集，则局部中的元素个数一定少于整体中的元素个数，但这个结论对于无限集合却不一定成立. 理想化状态下，我们可以把一滴水近似地看作是球形的，而太阳也近似地看作是球形的，二者区别之处是半径不同，“滴水含太阳”这句话从数量角度可以理解为“半径不同的两个球面上所含的点的个数是一样多的”，为了更好地理解这一点，我们设置了两个过渡问题.过渡问题 1: 长度分别为 2 cm 和 3 cm 的线段，哪条线段上的点多一些? 过渡问题 2: 半径分别为 2 cm 和 3 cm 的圆周，哪个圆周上的点多一些? 上述两个问题中，所涉及的点数都是相同的. 事实上，在过渡问题 1 中，我们假设图 1 的三角形中 a、b 两条线段分别长 2 cm 和 3 cm，借助三角形中的线段 c 可以建立线段 a、b 上的点之间的一一映射，两条线段上的点数是一样多的，可以断言线段上的点数的多少与线段的长度没有必然的联系，任意两条长度不同的线段上的点之间都可以建立一一对应关系，即任意两条不同线段上的点数是一样多的; 同理，任意两个半径不同的圆周上的点之间也可以建立如图 2 所示的一一对应关系，因此半径不同的任意两个圆周上的点数也是一样多的. 类比于两个过渡问题的求解，两个半径不同的球面上的点之间也可以建立一一对应关系，因此点数也是一样多的. 在上述问题的求解过程中，特殊的映射，也就是一一映射起了关键作用.

　　3 结束语

　　著名荷兰数学家、数学教育家弗赖登塔尔认为: 数学是依靠“就这样继续下去”和“一一对应”两大思想发展起来的[6]. 前者说的就是永无止境的极限过程，极限是一盏指引人们从“有限”走向“无限”的神灯; 后者说的是联系事物之间的对应方法，即特殊的映射———一一对应. 一一对应是管理混乱无序的无限世界的铁律，充分理解映射的概念，可以为更好地认识理解函数概念、研究函数性质奠定基础. 考虑到数学课程的重要性，不少文献对数学教学的教学方法、教学模式[7 - 9]进行了探讨，提出了学习数学的四种境界、问题牵引式教学方法等. 教无定法，教学是一个长期的、没有止境的探索过程，我们要在实践中不断提高教学水平，发现新的理论和方法.

　　参 考 文 献

　　[1] 同济大学数学系. 高等数学( 上册) [M]. 7 版. 上海: 高等教育出版社，2007: 1 - 2.

　　[2] 朱健民，李建平. 高等数学[M]. 北京: 高等教育出版社，2015: 13.

　　[3] DIFFIE W，HELLMAN M E. New directions in cryptography[J]. IEEE Transactions on Information Theory，1976，22( 6) : 644 - 654.

　　高等数学中映射概念的实例教学法相关论文期刊你还可以了解：《高等数学课程的混合式教学模式》

转载请注明来自：http://www.lunwenhr.com/hrlwfw/hrjylw/11559.html

文章TAG标签：高等数学论文