摘要 摘要:图的1-因子计数问题已经被证明是 NP-难的,但因该问题在量子化学、晶体物理学和计算机科学中都有重要的应用,对此问题的研究具有非常重要的理论价值和现实意义.首先,把图
摘要:图的1-因子计数问题已经被证明是 NP-难的,但因该问题在量子化学、晶体物理学和计算机科学中都有重要的应用,对此问题的研究具有非常重要的理论价值和现实意义.首先,把图的1-因子按关联某个顶点的边进行分类,求 出 每 一 类1-因子数的递推关系式.其 次,把各类1-因子的递推关系式相加,得到一组有相互联系的递推关系式,再利用这些递推关系式之间的相互关联,消去那些不需要的递推关系式,从而得到这个图的 1-因子数的递推关系式.最后解出这个递推关系式的通解,进而得到这个图的1-因子数的显式公式.
关键词:1-因子;递推关系式;通解;显式公式
0 引 言
理论上 讲,对 于 存 在1-因 子 的 图,把 1-因 子按照关联某个顶点的边进行分类,求 出 每 一 类1-因子数目,再把所有类求和就可以得到这个图的所有1-因子数.当这个图的顶点和边的数目较多时,这种方法就不是一个有效的方法(即计算量不是该图边数或顶点数的多项式计算量,而是指数表达式计算量).但是,利用这种思想,把这个图的所 有 1-因 子,按 照 饱 和 某 个 顶 点 的 1-因 子 分类,求出每一 类 1-因子数的递推关系式,再 把 各类1-因子的递推关系式相加,就得到一组有相互联系的递推关系式;利用这些递推关系式之间的相互关联,消去那些不需要的递推关系式,从而得到这个图的1-因子数的递推关系式;最后求出这个递推式的通解,进而得到这个图的1-因子数的显式公式[1-12].利 用 这 个 方 法 能 求 出1-因 子 递 推关系式的图是很多的,但能由递推关系式解出其显式表达式的图就比较有限了.原因是当递推关系式对应的特征方程是高次方程时,往往求不出其根.但是从 应 用 的 角 度 来 看,图 的 1-因 子 数 的递推关系式往往比其显式表达式更方便得到该图的1-因子数.因 此,这 个 方 法 为 图 的1-因 子 的 应用提供了有力支持.
1 基本概念
定义1 若图G 有一个1-正则生成子图,则称这个生成子图为图G 的1-因子.
定义2 设图G 是一个有1-因子的图,若图G 的两个1-因子 M1 和 M2 中有一条边不同,则称M1 和 M2 是图G 的两个不同的1-因子.
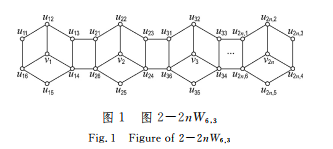
定义3 设Ci=ui1ui2ui3ui4ui5ui6ui1是长为6的圈,把顶点vi 与圈Ci 上的顶点ui2、ui4、ui6分别连接一条 边 的 图 记 为 Wi6,3 (i=1,2,…,2n).给Wi6,3与 Wi+16,3 的添加上边ui3ui+1,1、ui4ui+1,6(i=1,2,…,2n-1)得到的图记为2-2nW6,3,如图1所示.
定义4 设Ci=ui1ui2ui3ui4ui5ui6ui1是长为6的圈,把顶点ui2、ui4、ui6分别顺次连接一条边的图记为Xi6,3(i=1,2,…,n).给Xi6,3与Xi+16,3 的添加上边ui3ui+1,2、ui4ui+1,1、ui5ui+1,6(i=1,2,…,n-1)得到的图记为3-nX6,3,如图2所示.
先求g(n)的递推关系式.设图G1 的1-因子的集合为 M,则 M 中的1-因子按包含边xy、xw可划分为子集M1 和 M2,按照不同1-因子的定义有 M1∩M2=,M=M1∪M2,故 M = M1 +M2 .由f(2n)的 定 义,图 G1 的 包 含 边xy 和wz的1-因子数等于f(2n),即 M1 =f(2n).M2 中的1-因子按照包含边的情况可以划分3类.M2 中包 含 边xw、yz 的1-因子的集合记为M12;M2 中 包 含 边 xw、yu11、zu16、u12v1、u14u15、u13u21、u22u23、v2u26、u24u25的 1-因子的集合记为M22;M2 中 包 含 边 xw、yu11、zu16、u12v1、u13u21、u14u15、u25u26的1-因子的集合记为 M32.由f(2n)的 定 义 知,M12 =f(2n),M22 =f(2(n-1)).由g(n)的定义知,M32 =g(2(n-1)).因为 Mi2∩Mj2=(1≤i
2 主要结果
定 理 1 设 图 2-2nW6,3 的 1-因 子 数 为f(2n),则f(2n)=9·10n-1.证明 容 易 看 出 图2-2nW6,3有1-因 子.为了求f(2n)的 表 达 式,先 构 造 一 个 图 G1,并 求 它的1-因子数的递推关系式.将4圈xyzwx上的顶点y和z 分别与图2-2nW6,3的顶点u11和u16各连接一条边,得到的图记为G1,如图3所示.容易看出图G1 有1-因子,g(n)表示图G1 的1-因子数.
1-因子的集合为 M,按照 M 中元素饱和顶 点u11的情况可分两类:设 M 中包含边u11u12的1-因子的集合为 M1,M 中包含边u11u16的1-因子的集合为 M2.则 M1∩M2 =,M=M1 ∪M2,故 M =M1 + M2 .M1 可 分 4 类.M1 中 包 含 边 u11u12、v1u14、u15u16、u13u21、u25u26的1-因子的集合记为 M11;M1中 包 含 边 u11u12、v1u14、u15u16、u13u21、u22u23、v2u26、u24u25的1-因子的集合记为 M21;M1 中包含边u11u12、v1u16、u14u15、u13u21、u25u26的 1-因 子 的集合记为 M31;M1 中 包 含 边u11u12、v1u16、u14u15、u13u21、v2u26、u24u25、u22u23的 1-因子的集合记为M41;则 Mi1 ∩Mj1 = (1≤i
u13u21、u25u26的1-因子的集合记为 M22.由f(2n)的定义知,M12 =f(2(n-1));由g(n)的定义知,M22 =g(2(n-1)).因为 M12 ∩ M22 = ,M2 = M12 ∪ M22,所 以M2 = M12 + M22 .故 M2 =f(2(n-1))+g(2(n-1)).于 是, M = M1 + M2 =3f(2(n-1))+3g(2(n-1)),即f(2n)=3f(2(n-1))+3g(2(n-1)) (2)由式(1),得g(2(n-1))=2f(2(n-1))+f(2(n-2))+g(2(n-2)) (3)把式(3)代入式(2),得f(2n)=9f(2(n-1))+3f(2(n-2))+3g(2(n-2)) (4)由式(2),得f(2(n-1))=3f(2(n-2))+3g(2(n-2))(5)由式(4)和式(5)消去g(2(n-2)),得f(2n)=10f(2(n-1)) (6)由图4知,f(2×1)=9.由式(6),得f(2n)=10n-1f(2×1).故f(2n)=9·10n-1.
定理2 设图3-nX6,3的1-因子数为h(n),则h(n)=2·3n-1.证明 容易看出图3-nX6,3有1-因子.为了得到h(n)的表达式,构造图G2 并求出它的1-因子数的递推关系式.把路xy 的端点x、y 分 别 与图3-nX6,3顶点u12、u11连接一条边,得到的图记为G2,如图5所示.容易看出图G2 有1-因子,t(n)表示图 G2 的1-因子数.设图G2 的1-因子的集合为 M,图G2 包含边xy、xu12的1-因子的集合分别为 M1、M2,则M1∩M2 = ,M =M1 ∪M2,故t(n)= M =M1 + M2 .
因为 xy∈M1,所 以 xu12,yu11 M1,故 由h(n)的定义知,M1 =h(n).因为xu12 ∈M2,所 以yu11,u16u15 ∈M2,xy,u11u12,u11u16,u12u13,u14u15,u15u26M2,故由t(n)的定义知,M2 =t(n-1).因此t(n)=h(n)+t(n-1) (7)再求h(n)的递推关系式.设图3-nX6,3的1-因子 的 集 合 为 M,图 3-nX6,3 包 含 边 u11u12、u11u16 的1-因 子 的 集 合 分 别 为 M1、M2,则 M1 ∩ M2=,M=M1∪M2,故h(n)= M = M1 +M2 .由 于 图 3-nX6,3 具 有 对 称 性, M1 =M2 .因为u11u12∈M1,所以u15u16∈M1,且u11u16,u12u13,u12u14,u12u16,u14u15,u14u16,u15u26M1,故由t(n)的 定 义 知, M1 =t(n-1),故 M2 =t(n-1).因此h(n)=2t(n-1) (8)由式(7),得t(n-1)=h(n-1)+t(n-2) (9)把式(9)代入式(8),得h(n)=2h(n-1)+2t(n-2) (10)因此h(n)=3h(n-1)=…=3n-1h(1)由图6知,h(1)=2,故h(n)=2·3n-1.
3 结 语
图的1-因 子 计 数 理 论 是 图 论 研 究 的 重 要 内容之一,而且是一个有生机和活力的研究领域.它不仅有很强的应用背景,而且在过去的几十年中,它是快速发展的组合论中许多重要思想的源泉.本文给出的方法,不仅能求出很多类图的1-因子数的递推关系式,而且,对于顶点和边的数目不太多的图,还能 够 得 到 它 的 所 有 不 同 的 1-因 子.这些结果丰富了1-因子的计数理论,同时给1-因子的应用提供了支持.
参考文献:
[1] VALIANTLG.Thecomplexityofcomputingthepermanent[J].TheoreticalComputeScience,1979,8(2):189-201.
[2] 林 泓,林 晓 霞.若干四角系统完美匹配数的计算 [J].福 州 大 学 学 报 (自 然 科 学 版 ),2005,33(6):704-710.LIN Hong,LIN Xiaoxia.Enumerationofperfectmatchingsinsometypepolyminoes[J].JournalofFuzhouUniversity(NaturalSciences),2005,33(6):704-710.(inChinese)
[3] 唐 保 祥,李 刚,任 韩.3 类 图 完 美 匹 配 的 数目[J].浙江大 学 学 报(理 学 版),2011,38(4):16-19.TANG Baoxiang, LI Gang, REN Han. Thenumberofperfectmatchingforthreespecifictypesof graphs [J].Journal of Zhejiang University(Science Edition),2011,38 (4):16-19. (inChinese)
[4] 唐 保 祥,任 韩.4 类图完美匹配数目的递推求法 [J].数学杂志,2015,353(3):626-634.TANGBaoxiang,REN Han.Recursivemethodforfindingthenumberofperfectmatchingsofthefourtypesofgraphs[J].JournalofMathematics,2015,353(3):626-634.(inChinese)
两类特殊图1-因子数分类递推求法相关论文你还可以参考:《浅议初中物理学习困难的原因及对策》
转载请注明来自:http://www.lunwenhr.com/hrlwfw/hrsklw/11318.html